When finding a definite integral, do you spend an inordinate amount of time in the step-by-step algebra? Let’s say you are integrating over a probability of default function that has been fitted to real-life data (a non-normal curve) and you want to understand step-size dependence.
Or perhaps you are a beginning student of mathematical finance, reviewing the fundamentals of integration, and you just wish there was a faster way to change functions and spit out a graph.
“Integration is a summative process, and the applications that show this can become a time-sink,” said Robert Lopez, Emeritus Professor of Mathematics at the Rose-Hulman Institute of Technology, and author of Advanced Engineering Mathematics (Addison Wesley, 2001; now available as an ebook from Maplesoft). He was speaking at a webinar sponsored by Maplesoft on August 7, 2014, on using Clickable Calculus, a new paradigm for classroom use of the computational software from a major computer algebra system (CAS) developer.
“Students can get bogged down in the details of integration,” he said. Their interpretation of the word problem may be incorrect, but they will get stuck on evaluating an integral rather than focussing on what is truly at the heart of the problem.
During the course of the webinar, Lopez worked from a sheet of dozens of sample integration problems, to show in real time how quickly the answers could be obtained in the easy-to-use Maple interface.
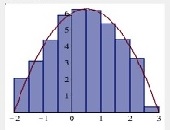
He began with Riemann sums and definite integrals. “You spend a lot of time teaching the algebra to find the Riemann sum,” said Lopez, and that leaves little time to explore the finer point that the definite integral is simply the limit of a Riemann sum.
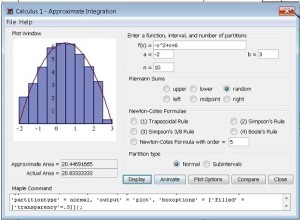
Lopez quickly progressed to the easy-to-use dialog box for approximate integration shown here.
In Lopez’s experience, “the typical calculus course teaches skills first, and concepts second,” but CAS software implemented in the Clickable Calculus style can cut through the initial barrier. While working on standard problems, he talked the audience through use of shortcut keys and context-sensitive menus such as how to form, move, and evaluate complicated expressions.
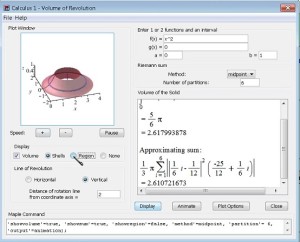
In another example, he compared different ways to obtain the volume of revolution. The menu path Tools>Tutors>Calculus Single Variable>Volume of Revolution produced the dialog box that had a variety of settings to manipulate.
For other worked problems, Lopez indicated some unique points of output in the Clickable Calculus interface. For example, imaginary numbers are indicated with an uppercase I, not the lowercase i.
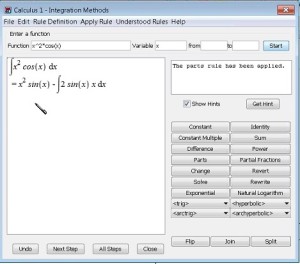
Some thoughtful touches appeared in the example of integration by parts. The Integration Methods dialog box allows the student to ask for hints. If an invalid method is selected, the dialog box displays a sentence explaining why the method was invalid. The student can ask for Next Step or All Steps (which produces a complete stepwise annotated solution).
“Integration by parts is really all about shifting the derivative from one factor in the integrand to the other,” said Lopez. In
Clickable Calculus, the Tutor requires that both u and v (not just dv) be specified. There is another tool in the interface designed so that the user only has to select the factor called u; Maple then infers the factor dv. The user might try a variety of factors for u. When the results appear, the Tutor automatically denotes what integration method was used, and what factors were selected for u and v.
At this time of year, students of finance at all levels may be brushing up on their calculus. Clickable Calculus engages students in a fun way as they explore new ways to work with the math. Students absorb the concepts, and they become comfortable with the CAS environment that can help them in their professional lives as they branch into solving “messy” problems. ª
Disclaimer: The author does not hold stock or any interest of a monetary nature in this software. Click here to see the comparison list of computer algebra systems.
The download link for the Calculus Study Guide is: http://www.maplesoft.com/products/studyguides/CalculusStudyGuide/index.aspx
The webinar presentation slides can be found at: http://www.maplesoft.com/lp/Maple15/clickable_calculus/player_webinar2.aspx
A link to recordings of more than 150 problems similar to those used in the webinar: http://www.maplesoft.com/teachingconcepts/
Links to recordings of similar webinars on other mathematical topics: http://www.maplesoft.com/lp/Maple15/clickable_calculus/